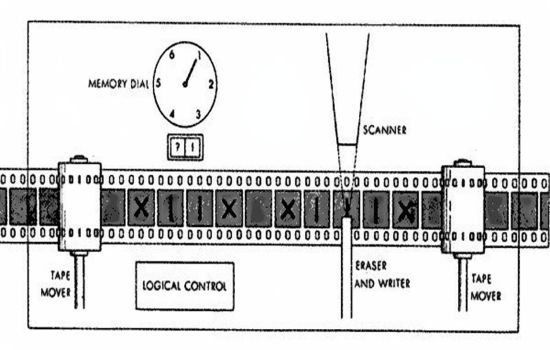
In November 1936, the British mathematician Alan Turing published the article „On Computable Numbers, with an Application to the Decision Problem“, in which he described a universal calculating machine. With only three operations, the machine was capable of all basic arithmetic operations. The machine was commonly called a Turing machine and later became one of the most important foundations in computer science. The first „Turing-capable“ machine was completed a few years after Turing’s article by Konrad Zuse with the Z3. In his 36-page article, however, Turing did not describe a real machine, but rather a theoretical construct. His machine had a memory with infinite space. He described the memory as a tape of arbitrary length, on which symbols can be written and from which they can also be deleted. The tape is an infinite tape running from right to left. The individual fields of the tape can be controlled with the read/write head. The processing for controlling the read/write head is always in a certain state and the processing itself is determined by a control program. Simply put, any algorithm can be executed with this machine. The machine is thus a small set of executable perations to transform an input into an output. The principle of reading a single character and writing another character in response is so simple and elementary that it can be implemented for almost any conceivable procedure. A computer can be programmed in this way to perform an infinite range of functions, provided that the human develops a method of describing that function. If the computer uses a suitable program, it can be used as a „brain for solving a particular task,“ as Konrad Zuse used to say.
